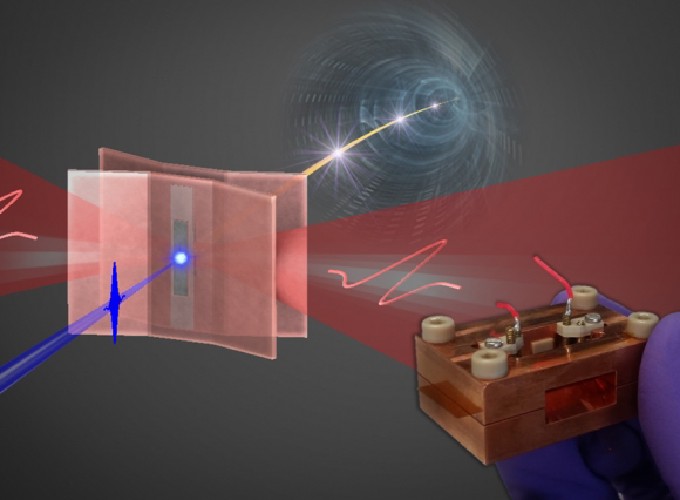
Overview
TL;DR We built an electron gun powered exclusively by THz radiation, marking the first demonstration of coherent electron acceleration from rest using laser pulses. We achieve state-of-the-art accelerating field, jitter, and produce electron bunches of suitable charge and energy spectra for low-energy diffraction experiments.
The ultimate goal of this project is to develop an end-to-end tabletop x-ray free electron laser (FEL) based purely on optical beams. Such a compact, economical FEL would bring the benefits of rarefied billion-dollar accelerator facilities to the local hospital (medical therapy with X-rays and electron beams) and university laboratory (understanding state transitions in metals, semiconductors, and molecules). This linear accelerator would be integrated with the THz-driven linear accelerator
The need for ultrafast electron guns
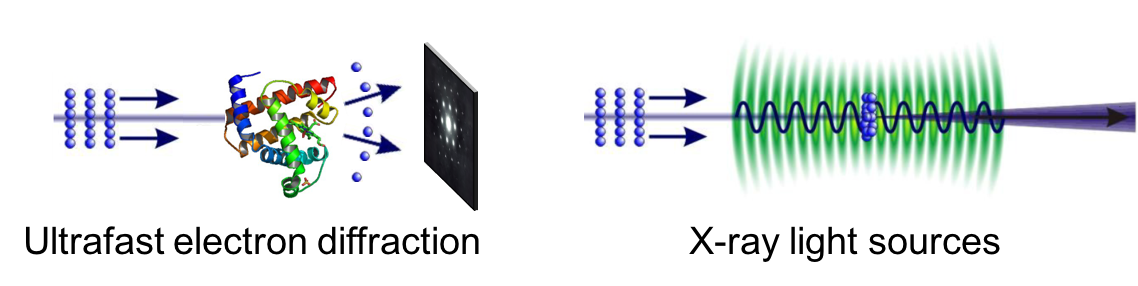
An electron gun is a device which emits and accelerates a narrow beam of electrons at a precise kinetic energy. They are used to ionize particles from an atom via electron ionization, a process commonly used in mass spectrometers. They are used to probe the dynamics of metals, semiconductors, and molecular crystals undergoing phase transitions via ultrafast electron diffraction. They are used in linear accelerators, producing the electron pulse which is accelerated to relativistic energies and converted to x-rays. The figure shows these latter two important applications.
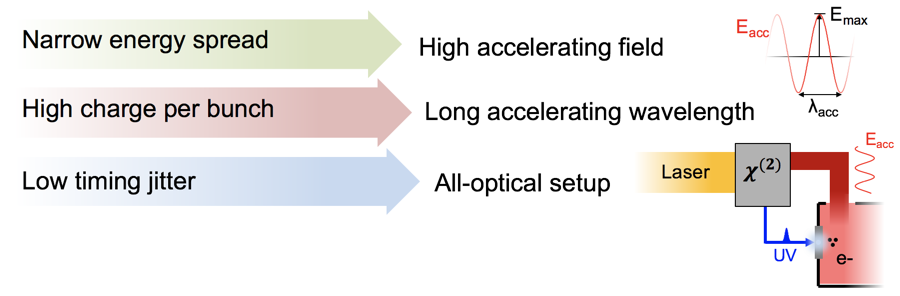
The performance of these systems often relies on having extremely good beam quality, energy spread, and jitter of the electron bunch generated from the gun. Low quality beams blur out the molecular structure captured by diffraction experiments, while low energy spread and high jitter leads to poor spectral- or time-resolution. Typically the higher the electric field on the electron bunch at the time of emission, the better the electron bunch will be, since it more quickly accelerates out of the nonrelativistic (slow) velocity regime where electron-electron Coulombic repulsion forces (space charge) ruin the beam’s integrity.
The need for THz fields
Performance
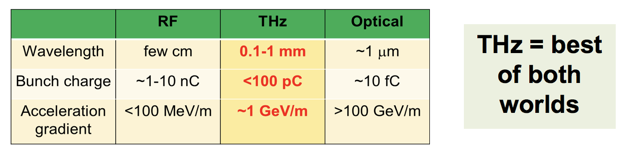
Conventional DC and RF electron guns have been hindered from producing high quality electron bunches due to their inability to produce high surface electric fields. Laser pulses have a significantly higher electric fields, but previous attempts to accelerate electron bunches using infrared lasers were limited in the volume of electrons that they can accelerate, due the short wavelength of the infrared spectral regime. Laser pulses in the THz regime, however, strike the best of both worlds. Optical THz pulses have extremely high field (GV/m), long accelerating wavelength, and zero jitter, making the THz spectral regime ideally suited for scientific electron gun applications. The figure below highlights the advantages of using THz radiation for electron acceleration.
Compactness
Further, due to the relative compactness of laser THz sources versus RF sources (large energy-hungry klystrons) and DC sources (bulky high voltage equipment), THz electron guns are significantly smaller and energy-efficient than conventional RF and DC based guns. In fact, the THz can be generated from the same laser as that of the photoemitter (the laser which ionizes electrons from the cathode), which is present in every electron For example, our electron gun demonstrated here is about the size of a matchbox.
A micrometer-scale structure for electron acceleration
Schematic
Before diving into the emission and acceleration mechanism, we show here an overview schematic of our setup. THz is generated by optical rectification of an infrared (IR) pulse in a lithium niobate (LN) crystal. The THz beam is coupled into the electron gun, which is about the size of a matchbox. The accelerated electrons exit the gun through a slit and are spectrally characterized by a retarded field analyzer (RFA).
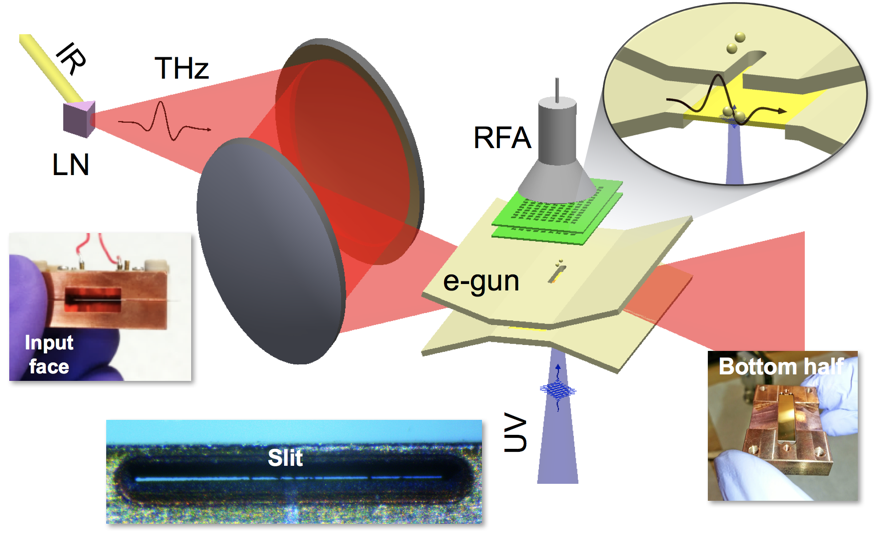
The challenge of accelerating electrons with an optical field is that the oscillating field accelerates and decelerates the electrons at a very high frequency (THz frequency, or a trillion cycles per second). If the electrons stay in place, they will gain zero net energy from the oscillating field since each accelerating cycle will cancel out each decelerating cycle. The trick is to design a structure that allows electrons to experience the accelerating half-cycle—then moves out of the way before the decelerating half-cycle which arrives less than one trillionth of a second later. That is the objective of our micrometer-scale structure shown in the figure above.
Sub-wavelength confinement of the THz wave
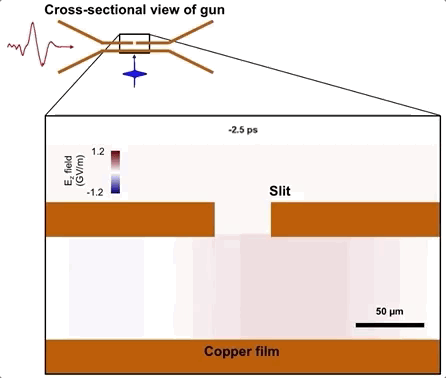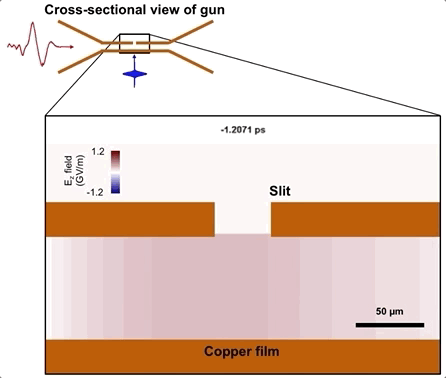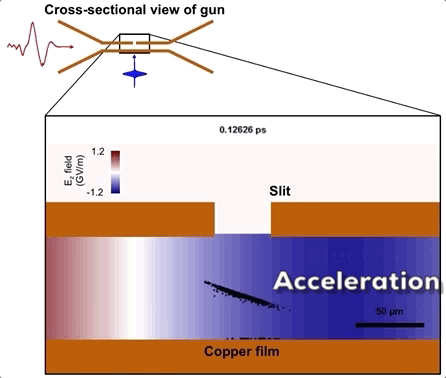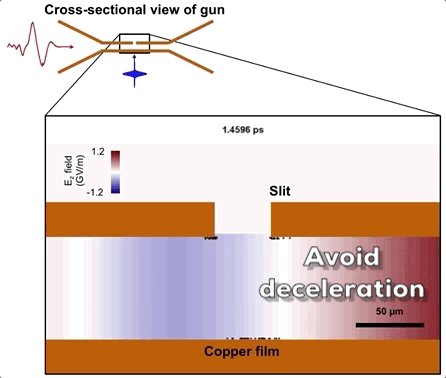
The structure acts as a waveguide for THz and a gun for electrons. We choose a waveguide gap of 75 $\mu$m in order to tightly confine the THz (by an order of magnitude below its wavelength) and hence enhance its field strength. Another reason for such a small gap is that the emitted electrons don’t have much time to escape the waveguide before the decelerating phase. The THz pulse is coupled into a THz waveguide by a butterfly-shaped tapering structure. Once inside the waveguide, the THz pulse travels in the TM0 mode with electric field orthogonal to the waveguide walls. Our finite-element simulation of the THz coupling into the waveguide is shown below.

Emission and acceleration of electron bunch
The electron bunch is emitted when a UV pulse back-illuminates one of these walls, which is only 30 nm thick. The bunch emits right at the beginning of the THz electric half-cycle and gets accelerated toward the other wall. It escapes the waveguide through a small slit at that wall just before the onset of the decelerating half-cycle. The figure below shows our particle tracking simulation of the dynamics.
Results
Finding the best operating point
An electron’s final momentum gain, $p_e$, depends on the time at which it is emitted with respect to the THz pulse, and it follows
$$ p_e=q\int_{t_{emit}}^{t_{exit}} E_{thz}(t) \mathrm{d}t. $$
where $t_{emit}$ and $t_{exit}$ are the times that the electron enters (through emission) and exits the waveguide, respectively. Thus, if $t_{exit}$ is much greater than the pulse duration of the THz pulse, the electron momentum gain will be a sinusoid 90 degree phase shifted from the THz wave. negative net momentum gain will result in the electron being recombined with the cathode, and such regions should result in low accelerated electron bunch charge and energy gain. We observe these results in the figure below, where we plot the electron energy gain and bunch charge as function of $t_{emit}$, or in practice the delay between THz and UV photoemitter pulse. The electron energy (bottom left) leads the THz wave (top left) by about 90 degrees as a function of $t_{emit}$.
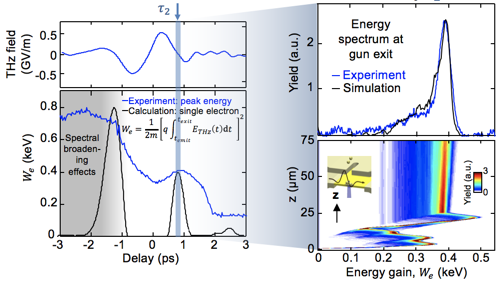
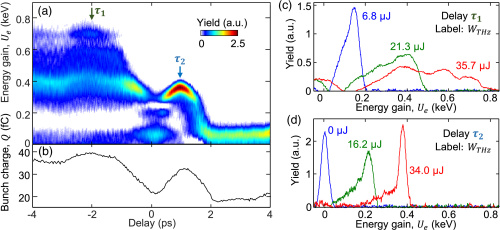
Note that the THz accelerating field exceeds 350 MV/m, which is 1.75 times higher than the best operating RF gun at SLAC National Lab. Two operating points are chosen for the electron gun, namely those at delays -1.5 ps and 0.8 ps. The operating point at 0.8 ps has especially nice electron spectra with a energy spread of only 5%. Our particle tracking simulations, which include the crucial effect of space charge, corroborate well with the observed spectrum (top right), and the bottom right plot shows a simulation of the acceleration dynamics. The raw spectra and bunch charge measurements as a function of delay are shown in the figure below.
Scaling up the THz energy
We turn our attention to seeing how the electron energy scales with increasing THz energy. Theoretically, the kinetic energy of the electrons $U_e$ follows the simple scaling law
$$ U_e = \frac{p_e^2}{2m} \propto E_{thz}^2 \propto W_{thz}$$
where the proportionality to $E_{thz}$ comes from the previous equation for the momentum gain of an electron. Thus, the electron energy should be proportional to the THz energy. We observe this is the case at both operating points of our electron gun as shown in the figure below.

All-optical low jitter
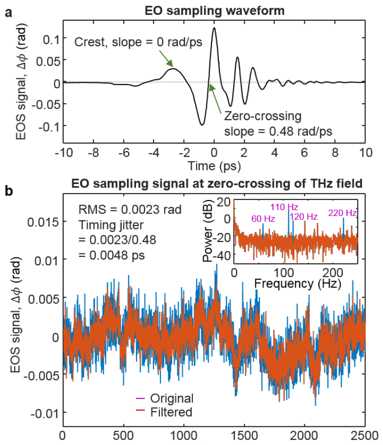
Because the UV pulse which emits the electrons comes from the same laser as the THz pulse which accelerates them, the entire system is all optical and achieves extremely low timing jitter without any no electronic synchronization of the pulses. We measure this jitter by using a infrared probe pulse to measure the THz field strength in an electro-optic sampling setup. We park the probe pulse at the zero-crossing of the THz field and collect 2500 measurements of the THz field over several seconds. After filtering out the noise spikes at the usual harmonics of 60 Hz and 110 Hz, we measured an RMS jitter of about 5 femtoseconds, which is significantly lower than that achievable by RF guns (about 100 fs at best).
Conclusion
This work shows the first demonstration of a THz electron gun. The all-optical low jitter gun has an accelerating field of 350 MV/m, which is higher than that achievable by RF guns. The accelerated electron bunch has an energy spread of about 5% and energy of about 0.4 keV which already suitable for low-energy electron diffraction experiments.