Overview
High energy ultrafast THz radiation is a key technology for national security (standoff detection of explosives), medicine (single-shot through clothing), basic science (nonlinear spectroscopy), and even charged particle acceleration. However, there exists a lack of efficient THz generation methods. My work on THz generation by a second order nonlinear optical process called optical rectification led to the demonstration of a THz source with >10x higher efficiency than current state-of-the-art. The result was achieved through a precise optimization of an elegant phase-matching technique called pulse front tilting. We then further increased the efficiency by 1.5x beyond our previous result by improving the nonlinear material properties through cryogenic cooling. Our systematic characterizations of the THz radiation abetted the development of the first complete systemic theory of THz generation by optical rectification. This level of analysis has opened up new understanding in THz generation and has served as a tool for developing newer, more efficient structures and methods.
The ultimate goal of this project is to develop an end-to-end tabletop x-ray free electron laser (FEL) based purely on optical (mostly THz) beams. Such a compact, economical FEL would bring the benefits of rarefied billion-dollar accelerator facilities to the local hospital (medical therapy with X-rays and electron beams) and university laboratory (understanding state transitions in metals, semiconductors, and molecules). This THz source would be integrated with the THz-driven electron gun and THz-driven linear accelerator
The THz gap
Uses of THz radiation
On the electromagnetic spectrum, THz radiation falls about one to two orders of magnitude above radio/microwave frequencies and about one to two orders of magnitude below optical/infrared frequencies. While both radio and optical frequencies possess a large number of generation techniques, there is a lack of efficient, high power sources in the so-called THz gap. This is unfortunate because the number of applications unique to THz radiation. Due to its intermediate wavelength, THz can penetrate through cardboard and clothing and perform medical, security, and industrial imaging with much higher resolution than radio frequency sources. Due to the many chemical signatures in the THz spectral regime, THz radiation can be used for both standoff detection of trace gases, as well as fundamental studies of chemical systems. The figure below highlights these applications of THz.
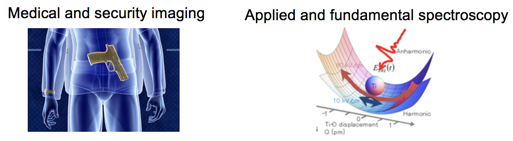
Finally, strong field THz pulses has found a new application in charged particle acceleration through our work on THz-driven electron guns and THz-driven linacs.
Pulsed THz generation techniques
We are interested in generating ultrashort THz pulses because of the need for a strong instantaneous field to accelerate electrons. Of the three most popular methods of generating such pulses (see figure below), we chose optical rectification for its scalability to higher energies. Optical rectification is a second order nonlinear optical process by which two optical/infrared frequencies mix nonlinearly to produce a difference frequency that lies in the THz regime. In order to conserve energy, another byproduct of the nonlinear mixing process is that the higher frequency IR component (the “signal”) gets redshifted to the frequency of the lower frequency IR component (the “idler”). The figure below illustrates how the mixing of two nonlinear infrared (IR) components produces a THz component via difference frequency mixing and causes the IR spectrum to be redshifted.
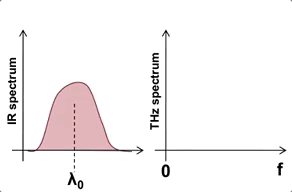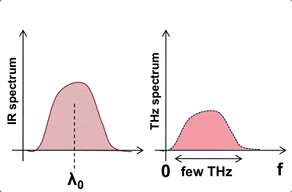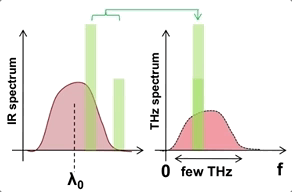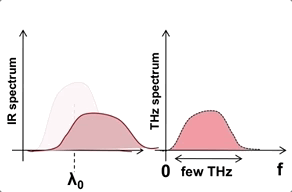
Due to the Manley-Rowe limit, the upper bound on the efficiency of this process is the ratio of frequencies between the generated THz and the lower of the infrared mixing components. This upper bound is extremely low, about 0.3%. We overcome this limit by a process called cascading, where we reuse the redshifted components to generate additional THz via successive optical rectification processes. Cascading can happen for $\sim$10 steps before the redshifted components are no longer phase matched with the THz field.
Tilted pulse fronts: a phase matching solution
In order for a nonlinear optical process to be effective, it must generate the nonlinear component (in our case the THz field) coherently, i.e. the phase of the previously generated field should match the phase of the newly generated field. If we represent the field generated at each step as a phasor, then all the phasors should have the same angle in order for their sum to be maximal. If the phases are not matched, then the generated fields will destructively interfere and the THz field will not build up in energy. The figure below illustrates phase matching in phasor (real-imaginary) space.

